MeshUDF: Fast and Differentiable Meshing of Unsigned Distance Field Networks

Benoit Guillard, Federico Stella, Pascal Fua

Paper

Code

Abstract

Unsigned Distance Fields (UDFs) can be used to represent non-watertight surfaces. However, current approaches to converting them into explicit meshes tend to either be expensive or to degrade the accuracy. Here, we extend the marching cube algorithm to handle UDFs, both fast and accurately. Moreover, our approach to surface extraction is differentiable, which is key to using pretrained UDF networks to fit sparse data.

Example

(a) [MC] on an ε>0 level set
(b) Meshing a point cloud
(c) Our procedure
The UDF of a pair of trousers is meshed by either (a) Marching Cubes [MC] on the ε>0 level set, (b) meshing a dense point cloud as in [NDF], or (c) our algorithm.
Using (a), the shape is inflated and artificially thickened (visible at the leg openings). With (b), the mesh is open but rough, and the procedure is slow. In contrast, our method (c) quickly obtains an open and regular mesh.

Approach

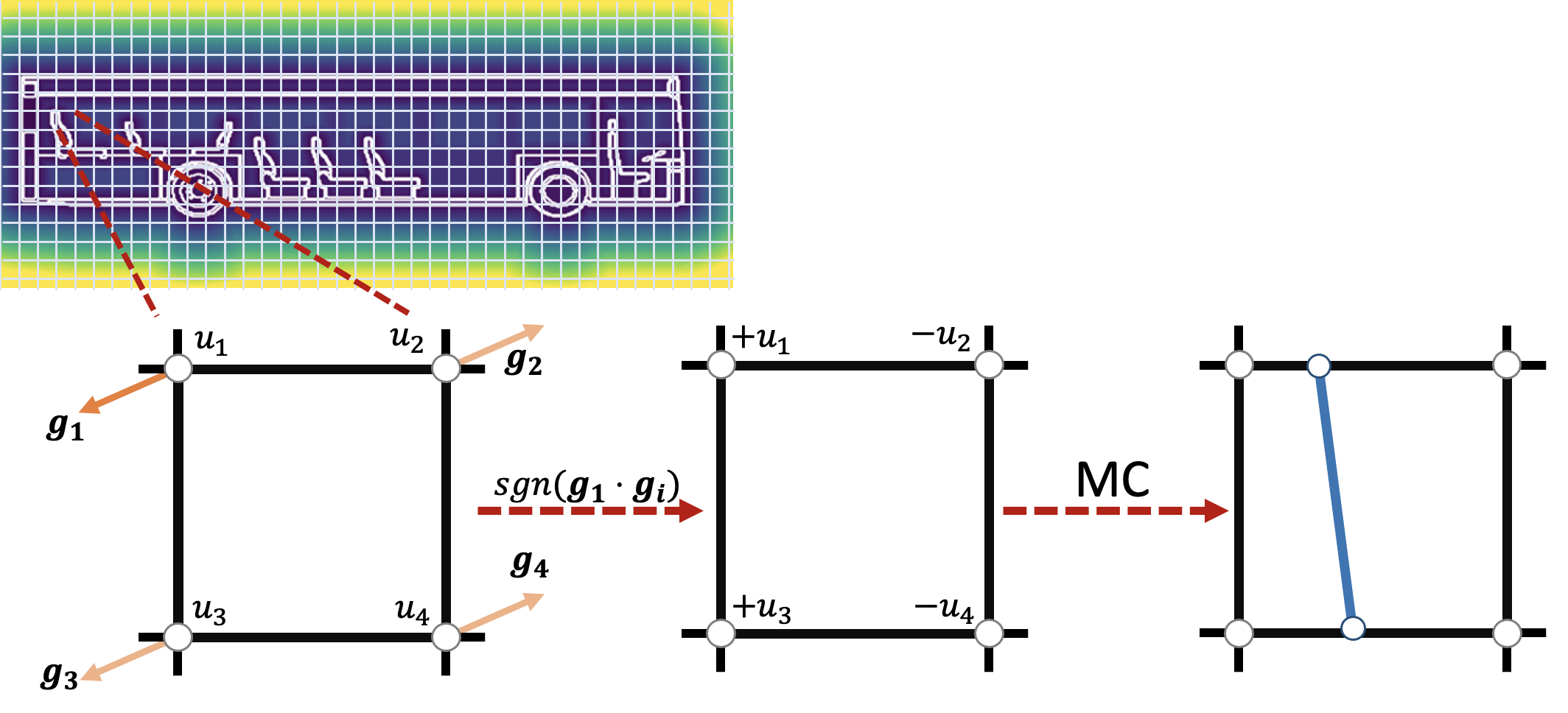
UDFs do not have sign flips, thus Marching Cubes [MC] does not apply directly. Instead, at each grid cell we rely on gradient orientations to infer local pseudo-signs. To ensure consistency between the pseudo-signs of neighboring grid cells, we explore the grid in a breadth-first manner.

Differentiability

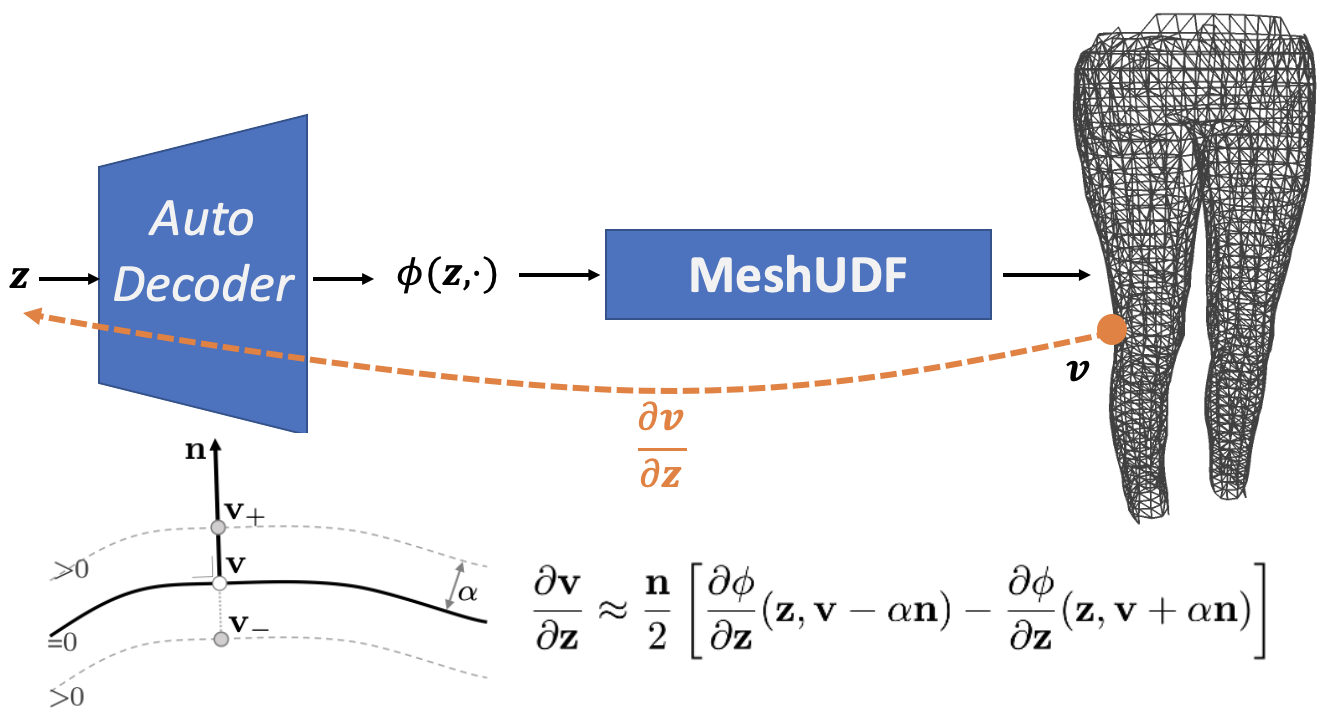
When the UDF φ(.) is decoded by a network from a latent code z, we provide gradients for mesh vertices v w.r.t. z. Since v lies at a singularity of the field, we control the α>0 level sets using differentiability results from [MS]. Intuitively, when the UDF increases at v- and decreases at v+, v moves in the direction of the normal n.

Optimization

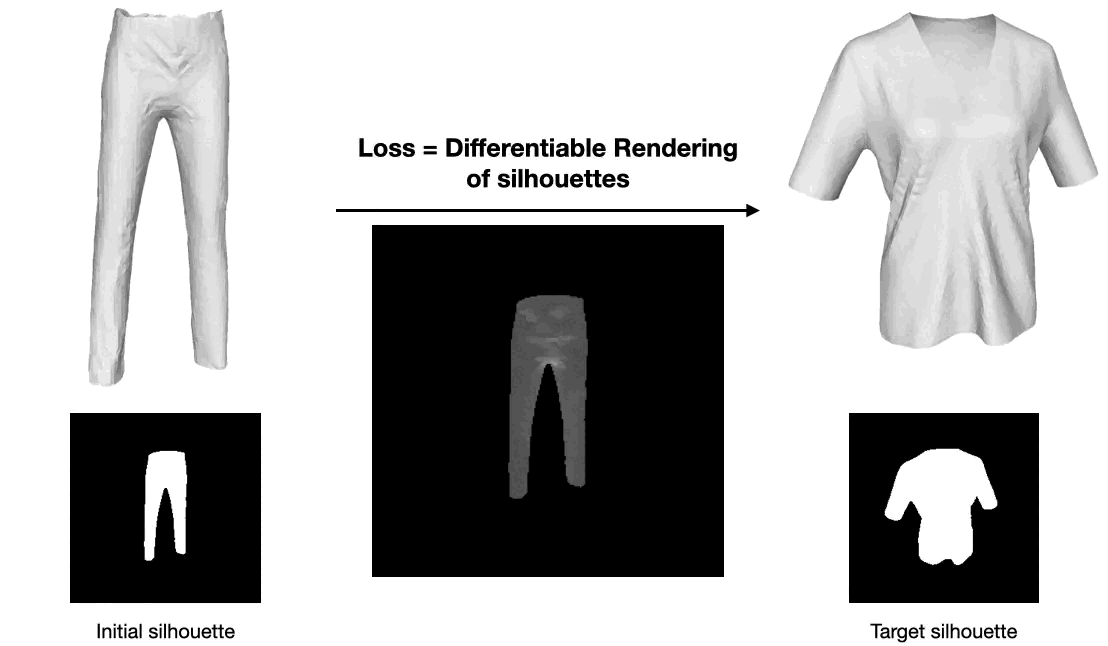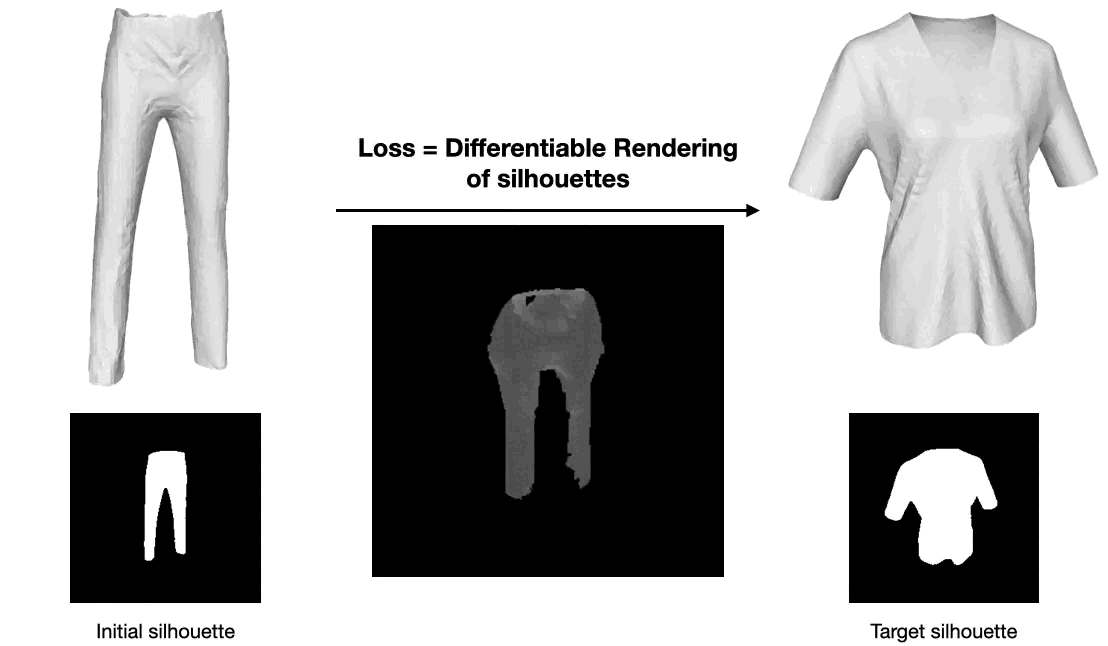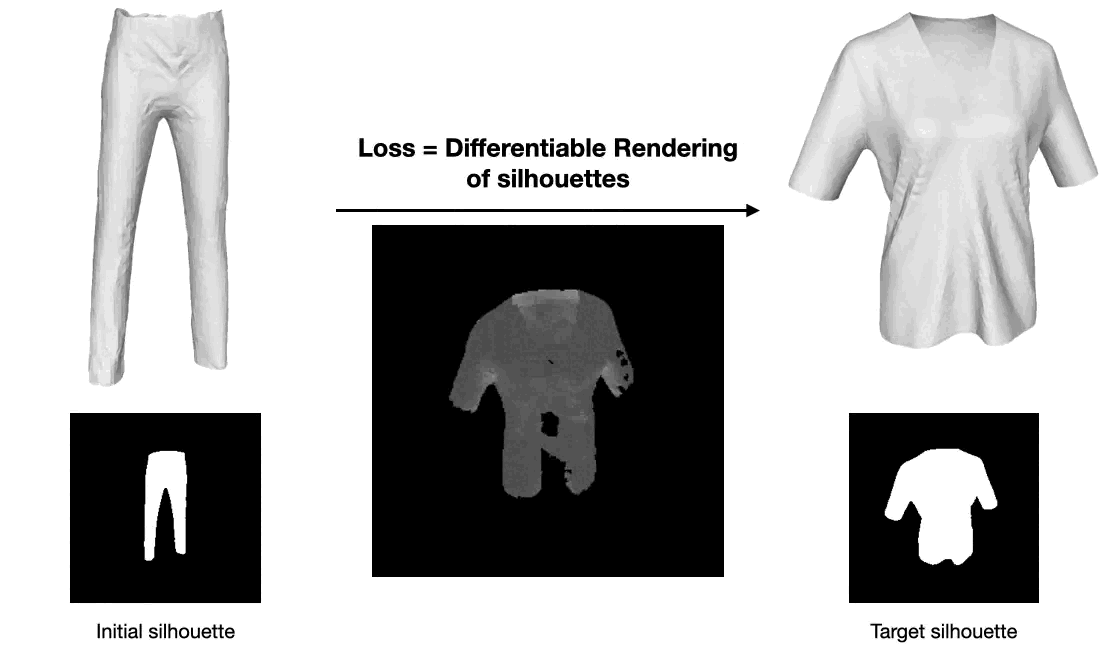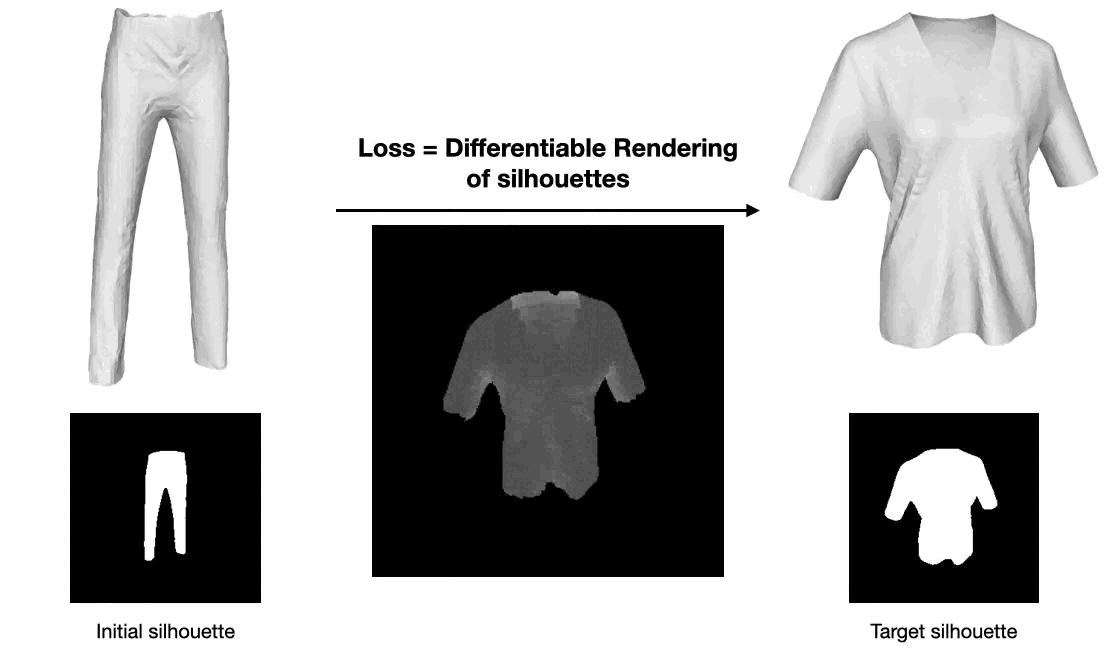
With the above gradients, a frozen UDF decoder can be used as a differentiable parameterization of open surface meshes. In this example, we start from the latent code of a pair of trousers, and optimize it so that the corresponding output mesh matches the silhouette of a tshirt.
Using our gradients and a differentiable rasterizer of meshes, we simply minimize a pixel space loss via gradient descent. The latent space traversal eventually results in a topology change.

BibTeX

If you find our work useful, please cite it:

@inproceedings{guillard2022udf,
  author = {Guillard, Benoit and Stella, Federico and Fua, Pascal},
  title = {MeshUDF: Fast and Differentiable Meshing of Unsigned Distance Field Networks},
  booktitle = {European Conference on Computer Vision},
  year = {2022}
}

References

[MC]
Marching Cubes: a High Resolution 3D Surface Construction Algorithm, Lorensen and Cline, SIGGRAPH 1987.
[NDF]
Neural Unsigned Distance Fields for Implicit Function Learning, Chibane et al., NeurIPS 2020.
[MS]
MeshSDF: Differentiable Iso-Surface Extraction, Remelli et al., NeurIPS 2020.